Surface, Deep and Transfer Learning in Math
As a follow up to last week’s blog, I thought I would write a little about the concepts of surface, deep, and transfer learning in mathematics and what they look like at school in our classrooms. Surface learning is when students learn new ideas and are taught about the concept, “and then, at the right time, labels and procedures are explicitly introduced to give structure to concepts”.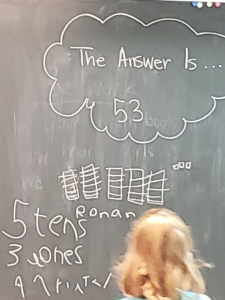
Surface learning can be explained by this example in grade 2/3. Students learn to represent numbers using the base ten blocks (a demonstration of the skill of decomposing numbers) – 5 tens, and 3 ones, to demonstrate they understand the concept of 53. They show that 5 tens plus 3 ones = 53, which is understanding that they can perform an operation with numbers to show how place value works (5 tens and 3 ones is 53, 50 + 3 + 53). They may also answer 60 – 7 = 53!
Through surface learning, students enlarge their toolbox of strategies to work with numbers and concepts. When students can choose the best method to solve a problem, or identify multiple ways to solve a problem, they are moving from surface learning to deep learning.
Deep learning is about making connections among ideas. Deep learning is about thinking such as “what is the most efficient way to solve this problem?” Or “what tool is the best for finding the answer to this problem?”
In the junior grades (4-6), deep learning looks like the understanding of arrays for multiplication ( 4 rows of 5 is 20) and connecting this to area – a rectangle with sides of 4 units and 5 units long has an area of 20 square units.
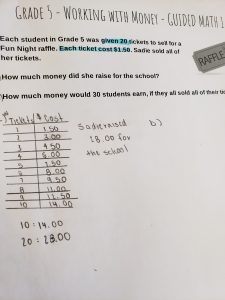
Above is an example of transfer learning. A problem is presented and the student needs to determine what strategy to use to solve the problem on their own. Here they use a chart (a strategy previously taught) to find the pattern that leads to the answer.
What problems can you think of at home?
Resource: Visible Learning in Mathematics, Hattie, John, Douglas Fischer and Nancy Frey, Corwin Mathematics, 2017.
Categories: Principal's Blog